

МЕТОДИКА АНАЛИЗА СТЕПЕНИ РЕГУЛЯРНОСТИ ЖИЛОЙ ЗАСТРОЙКИ СЕЛЬСКИХ ПОСЕЛЕНИЙ(Материал данного раздела опубликован в виде дипломной работы на тему "Разработка Web-сайта по памятникам архитектуры Архангельского Примошья" (Пояснительная записка) / Студ. - Боронин А.В., рук. Медведев П.П. ПетрГУ, Строительный факультет, кафедра "Систем автоматизированного проектирования". - Петрозаводск, 2004. - 110 с.:ил. (Архив кафедры "Систем автоматизированного проектирования" Строительного фпкультета Петрозаводского государственного университета)). При обследовании в качестве основополагающих выдвигаются три фактора, влияющих на регулярность объемно-планировочной структуры поселения. Первый фактор должен учитывать соотношение акцента со структурно-образующим элементом деревни, второй - разбросанность поселения в горизонтальной плоскости, третий - особенности рельефа. Остановимся наиболее подробно на установлении степени регулярности планировочной структуры в горизонтальной плоскости. Здесь могут существовать три вида отклонений от регулярности. Во-первых, отклонение азимута дома от перпендикуляра к дороге. Эта величина выражается в градусах. Во-вторых, отклонение расстояния от фасада дома до оси дороги от среднего. Дополнительное усреднение необходимо в данном случае для того, чтобы “отбить” так называемую “среднюю линию” для рассматриваемой деревни и отсчет расстояний вести от нее. Если не вводить этой поправки, то два варианта с одинаково выдвинутыми друг относительно друга домами, но расположенными в целом на разных расстояниях от дороги, дадут различные результаты. И, наконец, в-третьих, рассматривалось отклонение расстояний между домами от усредненного (по деревне) значения. Таким образом, первый показатель характеризует свободу постановки домов, ее независимость от упорядочивающего влияния дороги. Второй показатель прямо пропорционален степени разброса поселения в горизонтальной плоскости, что, естественно, является критерием нерегулярности планировки. Третий показатель характеризует сбой ритма при восприятии внутреннего пространства деревни. Чем выше этот показатель, тем больше степень аритмии в расстановке домов. На основании натурных измерений для каждой деревни заполнялась таблица, и по изложенной выше методике производился подсчет показателей. Для всех поселений находилась средневзвешенная величина отклонений. Безусловно, в упорядоченности поселений большую роль играет рельеф местности. Даже, схожие постройки, расставленные на различных по высоте перепадах, резко снижают ощущение регулярности объемно-планировочной структуры селений, но так как обследованные деревни находятся в одинаковых не только социально-экономических, но и природно-ландшафтных условиях, учетом рельефа с достаточной степенью объективности можно пренебречь. При последующем сравнении поселений других регионов потребуется введение поправочных коэффициентов, учитывающих особенности рельефа. Опыт проведения ареальных исследований показал, что при большом количестве вариантов исследуемого признака и при большом числе административно-территориальных единиц оперирование с полным набором данных при использовании только гистограмм довольно затруднителен, а порой и просто не дает никакого эффекта. Поэтому для познания внутренних закономерностей в многомерных распределениях чаще используются не графики, а специально рассчитываемые сводные итоговые меры. К их числу относится, в частности, величина, именуемая “средней” (М), которая обычно характеризует центральную тенденцию вариационных рядов. В историко-архитектурной статистике применительно к процентным вариационным рядам эта величина может быть также использована в качестве меры явной типичности исследуемых вариантов признака. Но необходимо помнить: чтобы средняя величина была действительно обобщающей, улавливающей закономерность, она должна применяться к достаточно однородной совокупности. Однако опыт работы с историко-архитектурными материалами свидетельствует, что такие случаи очень редки. Поэтому при характеристике неоднородных вариационных рядов требуется еще расчет таких мер, как “вариационный размах” (R) и “среднеквадратичное (или стандартное) отклонение”(G). И если одинаковы средние (М), то колеблемость больше у того признака, у которого больше G. Наконец, при случае сравнения двух распределений между собой при неравенстве их средних используется обычно коэффициент вариации (C). Но специфика архитектурно-типологических исследований заключается не только в сложном характере распределения вариационных рядов. Так, на начальном этапе анализа при оценке общего характера распределения вариантов конкретного исследуемого признака нередко возникает потребность в оценке типичности и уникальности каждого из выявленных вариантов. Ранее уже упоминалось, что такая мера как “средняя” (М) позволяет вычленить явно типичные и наиболее типичные варианты. Вопрос же об оценке уникальности вариантов (объектов) долгое время оставался открытым. Попытка разрешить эту задачу на конкретных примерах из практических исследований показала необходимость разработки специальной меры оценки уникальности. В качестве исходного постулата была взята математическая идея оценки вариации не метрических, а классификационных признаков с помощью различия в качестве на базе искусственно сконструированной специальной нормированной меры. Однако использование данной меры “впрямую” (без модификации) уже не позволяет разрешить историко-архитектурную задачу однозначно, поскольку в этом случае оценивается вариация в целом, а не вклад каждого класса (варианта) в эту вариацию. В данной ситуации было предложено перейти к процентному (а не частотному) соотношению и на его основе определить процентную меру перехода от типичности к уникальности для каждого из классов (вариантов). Опуская соответствующие выкладки, приведем только конечный результат: процентная мера перехода от типичности к уникальности для трех, четырех, пяти и шести классов (вариантов) составляет соответственно, 9.76%, 8.17%, 5.86% и 2.96%. Именно в такой своей форме данная мера и была апробирована, к примеру, при проведении ареальных исследований деревянного зодчества Онежского бассейна. В дополнение к сказанному отметим, что, несмотря на внешне частный характер рассмотренной выше проблемы, при ее успешном разрешении открывается довольно широкий простор для новых научно-теоретических изысканий. В частности, по мере накопления соответствующих конечных результатов по всему известному набору типологических признаков и при условии решения проблемы выбора “весовых” мер в перспективе возможно создание достаточно полного кадастра на объекты деревянного зодчества, базирующегося на объективизированных оценках их историко-культурной ценности. С другой стороны, рассмотренный выше переход от коэффициента вариации качественных признаков к процентной мере не следует рассматривать как отказ от использования первого в историко-архитектурной статистике. С учетом смыслового содержания коэффициент вариации может быть успешно применен при оценке приоритетов в выборе тех или иных форм, приемов и деталей различными этническими группами населения и особенно при изучении зон этнических контактов. Результаты расчета элементарных статистик и ранжирования исходных историко-архитектурных данных являются базой при выработке научно-теоретических гипотез, для подтверждения которых далее могут использоваться более сложные математико-статистические методы, и в частности, корреляционный анализ - изучение зависимости между двумя и более признаками. Основой такого анализа является следующее теоретическое положение: если данному значению одной величины соответствует вполне определенное значение другой, то говорят, что между этими величинами имеет место функциональная зависимость. В общем, случае она представима в виде уравнения: 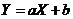
и отображается прямолинейным графиком. Однако далеко не всегда зависимость может иметь столь простой (или относительно простой) характер. Пример - график “корреляционного облака”, отражающий тенденцию возрастания (положительная корреляция) или убывания (отрицательная корреляция) одной переменной при возрастании другой. Говоря о функциональной и корреляционной зависимостях, заострим внимание на двух важных моментах. Во-первых, обе зависимости могут быть, а могут и не быть причинно-следственными. Логическая природа рассматриваемых “сечений” (функциональная — корреляционная и причинно-следственная — не причинно-следственная) принципиально различна. Во-вторых, если при функциональной связи в упрощенных ситуациях (при абстрагировании от ряда явлений) можно говорить о причинной зависимости, то в случае корреляционной связи все значительно сложнее. Здесь любое явление находится под влиянием большого числа факторов, каждый из которых имеет, вообще говоря, различную “силу”. В этом случае наличие корреляции свидетельствует, что либо одно из двух исследуемых явлений есть частичная причина другого, либо оба явления - следствие общих причин. Наглядной иллюстрацией практически всех начальных этапов корреляционного анализа и его возможностей может служить одна из практических задач, решенных в процессе проведения ареальных исследований деревянного зодчества Онежского бассейна - оценка характера распределения вариантов домов-комплексов с последовательной связью по двум административным районам. Первоначально была сформулирована рабочая гипотеза о существовании связи между анализируемыми признаками и построена исходная корреляционная таблица при условии, что распределение объектов по клеткам таблицы, очевидно, зависит от характера связи между признаками. Для оценки предполагаемой связи данная эмпирическая таблица была сопоставлена с теоретической, построенной на основании гипотезы об отсутствии связи между анализируемыми признаками. Построение теоретической таблицы можно осуществить вручную, вычисляя внутриклеточные частоты по формуле: 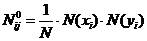
В качестве меры отклонения в этом случае использовался далее критерий χ (хи-квадрат), предложенный Пирсоном: 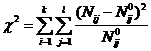
В силу разного рода случайных обстоятельств наполнение клеток эмпирической таблицы может отличаться от наполнения теоретической, даже в том случае, когда эмпирическое распределение в принципе соответствует теоретическому. Чтобы ответить на вопрос, носит ли отклонение таблиц случайный характер, вводят два показателя: показатель степени значимости (q) и показатель числа степеней свободы корреляционной таблицы (f). Поскольку разговор идет о cлучайных событиях, то утверждение о расхождении таблиц высказывается с определенной вероятностью (p). В технических науках p = 0,99 (q= 1-p= 0,01), а в социальных и исторических исследованиях p = 0,95 (q= 1-p= 0,05). Степень свободы корреляционной таблицы определяется как: 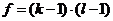
Для разных q и f составлены специальные математические таблицы, по которым можно найти величину χ [Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1977,с. 465, прил. 5; 12, с. 258, табл. Б], обладающую таким свойством: для данной корреляционной таблицы (χ, f) с вероятностью p=(1—q) можно утверждать, что отклонение теоретической таблицы от эмпирической носит случайный характер, если: 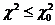
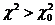
До сих пор речь шла о теоретических таблицах, построенных на основе гипотезы независимости, т. е. решался вопрос, есть ли связь между признаками. Однако теоретическая таблица может быть построена и на основе предполагаемого характера распределения. Во-первых, на основании некоторой содержательной теории. Из теории определяется, каким должно быть соотношение вариантов, а затем с помощью критерия χ показывается соответствие эмпирических частот теоретическим. Данный прием может быть использован при анализе типологических признаков в различной этнической среде. В частности, в качестве теоретической таблицы могут выступать данные ранее обследованных с достаточно достоверной “чистотой” этнических приоритетов. Во-вторых, из гипотезы о характере распределения признаков. Таким путем можн проверить, соответствуют ли полученные данные предположению о нормальности распределения изучаемого признака (т.е. подпадают ли под общетеоретические законы). В эту же группу, видимо, войдут в перспективе задачи, связанные с изучением хронологической и территориальной динамики смены форм приемов и деталей. В-третьих, χ критерий дает возможность также сравнивать два ряда распределений и решать вопрос, случайно или нет различие между ними. Например, можно сравнивать распределение вариантов домов-комплексов и их этажности, что выполнено ниже. Таким же способом можно сравнивать распределения признаков в различной этнической среде. Возвращаясь вновь к таблице, отметим, что после установления статистического факта наличия связи между вариантами домов-комплексов и районами возникла потребность в описании характера этой связи. Для этой цели были использованы коэффициенты, базирующиеся на критерии χ Пирсона: коэффициент средней квадратической сопряженности Пирсона, а также средняя квадратическая сопряженность или “фи-мера связи”. Она характеризует степень различия между эмпирической и теоретической таблицами, приходящуюся на одно наблюдение: 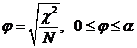
|
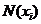 - маргиналы (итоги) по X
- маргиналы (итоги) по X
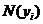 - маргиналы (итоги) по Y
- маргиналы (итоги) по Y
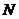 - общее число исследуемых объектов
- общее число исследуемых объектов
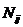 - маргиналы (итоги) по X
- маргиналы (итоги) по X
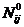 - маргиналы (итоги) по Y
- маргиналы (итоги) по Y
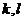 - общее число исследуемых объектов
- общее число исследуемых объектов